코드스테이츠 - 3회차 백엔드 부트캠프/Section 2

2022.09.27 화 - 의사코드, 시간 복잡도, 탐욕 알고리즘

곰돌이볼 2022. 9. 27. 09:47

📄 학습내용

알고리즘(Algorithm)

  • 알고리즘 : 문제를 해결하는 최선의 결과을 구하는 것 
  • 단계
    1. 문제 이해하기
      문제의 설명, 입출력, 제한 사항, 주의 사항 등 숙지하기
    2. 전략 세우기
      문제 해결에 적합한 알고리즘 선택하기
      의사코드 작성하기 
    3. 코드 작성하기

 

의사코드(pseudo code)

  • 의사코드 : 일상적인 언어로 코드의 동작이나 논리를 작성하는 것
  • 의사코드를 구체적으로 작성해야하는 이유 : 코드 작성 시 실행에 문제 없이 동작 가능
  • 장점
    1. 시간 단축
    2. 디버깅 용이
    3. 프로그래밍 언어를 모르는 사람과 소통 가능
  • 좋은 의사코드 특징
    1. 자신만의 원칙 세우기
    2. 일관성
    3. 다른 사람이 이해 가능해야 함
  • 작성방법
    1. 자연어
    2. 자연어 + 프로그래밍 언어

 

시간 복잡도(time complexity)

  • 시간 복잡도 : 입력값(N)에 따른 연산 횟수
    • 프로그램의 성능을 판단하는 지표로 사용
  • 표현 방법
    1. 빅오 표기법(Big-O) : 가장 최악의 연산 횟수를 고려한 표기 방법
      • 프로그래밍을 할 때에는 최악의 경우도 고려해야 하기 때문에 시간 복잡도에서 주로 사용하는 표현 방법
    2. 빅오메가 표기법(Big-Ω) : 가장 최소의 연산 횟수를 고려한 표기 방법
    3. 빅세타 표기법(Big-θ) : 최소와 최악의 평균적인 연산 횟수를 고려한 표기 방법
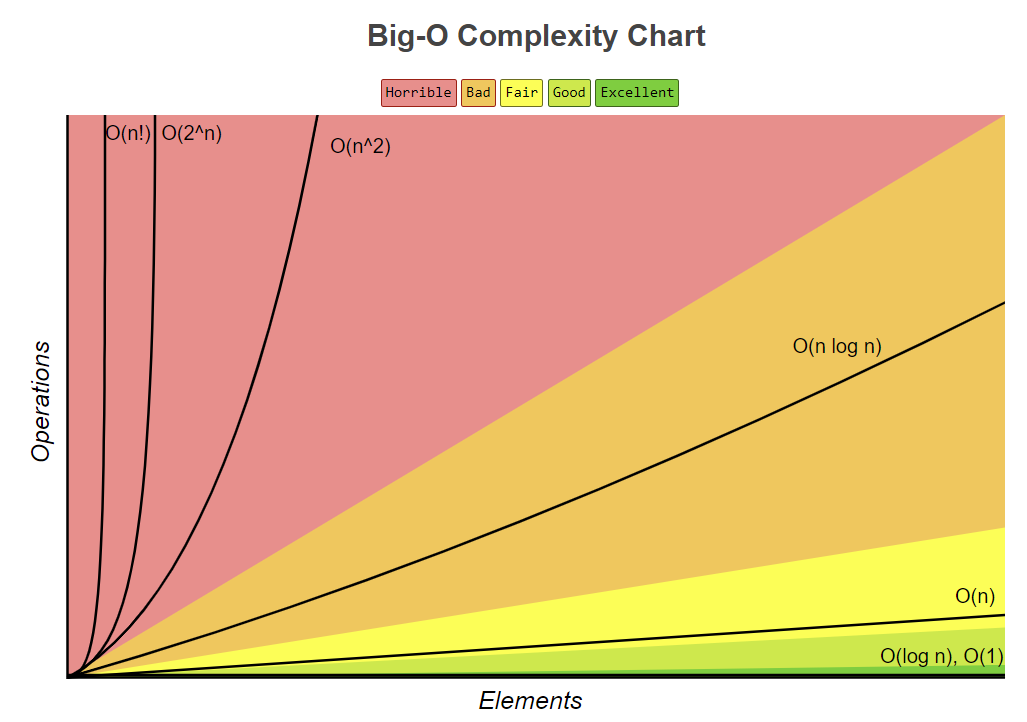
  • 빅오 표기법
    • O(1) : 입력값과 상관 없이 연산 횟수가 일정(constant complexity)
    • O(n) : 입력값에 따라서 연산 횟수가 비례적으로 증가(linear complexity)
    • O(log n) : BST와 같은 로직의 시간 복잡도(logarithmic complexity)
    • O(n2) : 입력값의 제곱수로 연산 횟수의 비율이 증가(qudratic complexity)
    • O(2n) : 2의 배수 형태로 연산 횟수가 증가(exponential complextiy)

출처 : https://www.bigocheatsheet.com/

 

탐욕 알고리즘(Greedy)

  • 탐욕 알고리즘 : 매순간마다 최적의 해답 선택을 통해서 최종적으로 문제를 해결하는 알고리즘 방식
    • 항상 최적의 해답을 도출하지 않음, but 최적과 근사한 값을 빠르게 도출
  • 단계 
    1. 선택 절차(Selection Procedure) : 매순간 최적의 해답 선택
    2. 적절성 검사(Feasibility Check) : 선택한 해답이 문제의 조건과 일치하는지 검사
    3. 해답 검사(Solution Check) : 해답이 최종 문제를 해결되면 종료, 아니면 1번 과정부터 반복
  • 탐욕 알고리즘 적용 조건
    1. 탐욕적 선택 속성(Greedy Choice Property) : 이전 상황의 선택이 이후 상황에 영향 X
    2. 최적 부분 구조(Optimal Substructure) : 문제를 작은 문제로 나누어 해결하는 방식을 통해서 최종적으로 문제 해결하는 방식

 

완전 탐색 알고리즘(Brute-Force Alogrithm)

  • 완전 탐색 알고리즘(Brute-Force Algorithm)  : 모든 경우의 수를 확인해서 문제를 해결하는 방식(시행착오 방법론)
    • 시간ㆍ공간 복잡도를 고려하지 않고 최악의 경우를 통해서라도 문제를 해결하려고 함
    • 문제의 복잡도 ↑  ∝ (시간 복잡도, 자원) ↑
  • 사용하는 경우
    1. 사용할 수 있는 적절한 알고리즘이 없는 경우
    2. 모든 경우의 해답을 확인해야 하는 경우
  • 사용되는 알고리즘
    • 순차 검색 알고리즘(sequential search) : 배열에서 특정 값 검색
    • 문열 매칭 알고리즘(brute-force string matching) : 길이가 N인 문자열에서 길이가 M인 문자열의 포함 여부 탐색
    • 선택 정렬 알고리즘(selection sort)
    • 버블 정렬 알고리즘(bubble sort)
    • tree 자료구조의 완전 탐색 알고리즘(DFS, BFS)
    • 동적 프로그랭(DP, Dynamic Programming)

 

이진 탐색 알고리즘(Binary Search Alogrithm)

  • 이진 탐색 알고리즘(Binary Search Algorithm)  : 정렬된 데이터에서 절반씩 나누어서 분할 정복기법으로 탐색하는 알고리즘
  • 한계 
    • 배열을 통해서만 구현 가능
    • 배열을 정렬해야 이진 탐색 알고리즘 적용 가능
  • 동작 단계

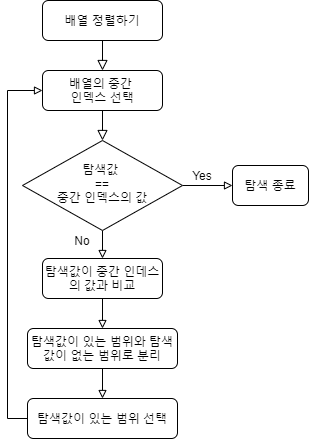
  • 시간 복잡도 : O(log N)
  • 사용되는 경우
    1. 사전에서 단어 검색
    2. 도서관에서 도서 검색
    3. 대규모 시스템의 리소스 사용 현황 파악
    4. 반도체 테스트 프로그램의 디지털 & 아날로그 레벨 측정

 

구현(implement)

  • 구현 : 생각한 로직을 코드로 작성하는 것
  • 구현 능력 검증 방법
    1. 완전 탐색(brute force) : 모든 경우의 수를 확인해서 문제를 해결하는 방법
    2. 시뮬레이션(simulation) : 문제의 복잡한 요구 사항을 코드(과정, 조건)로 구현해서 나온 결과를 확인하는 방법

 

🧶 발생한 문제 및 해결방법

  • 문제점) Ingeter 배열 역순
  • 해결방법) Integer 배열을 리스트로 변환해서 Collections.reverse() 메서드 이용
// Integer[] 배열
Integer[] arr = { 1, 2, 3 };
List<Integer> list = Arrays.asList(arr); // 배열(int X) → List
Collections.reverse(list); // Collections.reverse() 메서드를 이용해서 역순으로 만들기
Integer[] reverseArr = list.toArray(arr); // List → 배열

 

  • 문제점) int 배열 오름차순 정렬
  • 해결방법) stream 이용 또는 Arrays.sort() 메서드 사용
int[] arr = { 1, 2, 3 };

// 스트림으로 오름차순 정렬
int[] sortArr = Arrays.stream(arr)  // IntStream
        .sorted() // 오름차순 정렬
        .toArray(); // int[]
        
// Arrays.sort() 메서드 사용
Arrays.sort(arr);

 

  • 문제점) int 배열 내림차순 정렬
  • 해결방법) int 배열을 Integer 배열로 변환 후 Arrays.sort() 메서드 이용해서 내림차순 정렬, 정렬 후 Integer 배열을 int 배열로 변환
// 내림차순으로 정렬
int[] arr = { 1, 2, 3 };
Integer[] IntegerArr = // int 배열을 Interger 배열로 변환
        Arrays.stream(arr) // IntStream
                .boxed() // Stream<Integer>
                .toArray(Integer[]::new); // Interger[]
Arrays.sort(IntegerArr, Comparator.reverseOrder()); // 내림차순으로 정렬
int[] reverseArr = Arrays.stream(IntegerArr) // Stream<Integer>
        .mapToInt(i -> i) // IntStream
        .toArray(); // int[]

 

  • 문제점) int 배열을 Integer 배열로 변환/Integer 배열을 int 배열로 변환
  • 해결방법) 
// int[] → Integer[]
int[] arr = { 1, 2, 3 };
Integer[] IntegerArr =
        Arrays.stream(arr) // IntStream
                .boxed() // Stream<Integer>
                .toArray(Integer[]::new); // Interger[]

// Integer[] → int[]
arr = Arrays.stream(IntegerArr) // Stream<Integer>
        .mapToInt(i -> i) // IntStream
        .toArray(); // int[]

 

⭐ 공부 난이도

탐욕 알고리즘, 시간 복잡도 ☆☆☆☆★ 

 

🌕 느낀점

  코테 준비할 때, 탐욕 알고리즘을 이용해서 문제를 해결하는 것이 어려웠던 것으로 기억된다. 오늘은 구현을 안하고 이론만 공부해서 그런지 큰 어려움은 존재하지 않았다. 시간 복잡도와 이외의 여러 가지 알고리즘을 복습할 수 있어서 좋았다. 안 좋은 버릇인 생각없이 그냥 유어클래스의 글을 읽고 있었다. 머리를 쓰지 않고 공부하는 것을 유의해야겠다. 공부를 할 떄 이해를 하면서 외우도록 의식할 수 있도록 노력해야겠다.

 

 

저작자표시 (새창열림)